مکانیزم کنترل ربات دیفرانسیلی
انواع و اقسام مختلفی از چرخ ها در بازار وجود دارد . اما هنگامی که چرخی برای ربات خود انتخاب می کنید باید به فکر برنامه ای برای کنترل آن چرخ نیز باشید . در این نوشتار به بررسی مکانیزم دیفرانسیلی جهت کنترل و هدایت ربات می پردازیم .
مکانیزم کنترلی دیفرانسیلی :
این مکانیزم کنترل ربات رایج ترین نوع مکانیزم های ربات به ویژه برای تازه کارهاست . مفهوم این مکانیزم نسبتاً ساده تر است . تفاوت سرعت بین دو موتور ربات را در مسیر و جهت مورد نظر هدایت می کند . نام گذاری این روش نیز به همین تفاوت سرعت بر می گردد . (Velocity difference) واژه difference به معنای اختلاف و تفاوت ، که Differential از آن گرفته شده و به معنای اختلاف یا تغییرات است .
در این مدل مکانیزم ربات می تواند دو چرخ مستقل داشته باشد و یا دو چرخ اصلی با محور افقی که هر یک به وسیله یک موتور مجزا حرکت می کند و یک چرخ غلتکی که به عنوان هرزگرد و به منظور حفظ تعادل به کار می رود ، در برخی موارد نیز بسته به نیاز ممکن است ترمز هم داشته باشد . پس بخش اصلی این مکانیزم شامل موارد زیر است :
| اجزاء اصلی مکانیزم دیفرانسیلی ربات | |
| اجزاء | تعداد |
| موتور | 2 |
| چرخ | 2 |
| پلتفرم (صفحه شاسی ربات) - بدنه ربات | 1 |
| هرزگرد (در صورت نیاز به حفظ تعادل) | 1 |
3 مورد اساسی در ربات هایی با مکانیزم دیفرانسیلی اتفاق می افتد :
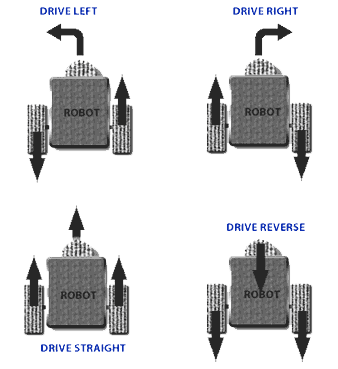
( برای مبتدی ها )
- اگر سرعت خطی چرخ ها یکسان باشد یعنی هر دو چرخ در یک جهت (جلو یا عقب) حرکت کنند و مقدارشان هم یکی باشد ربات حرکتی مستقیم و خطی خواهد داشت .
- اگر سرعت از نظر اندازه یکسان ولی از حیث جهت متفاوت باشد ، یعنی هر دو چرخ با یک سرعت در حال حرکت باشند ولی جهت حرکتشان خلاف هم باشد (یکی به سمت جلو و یکی به سمت عقب) آن گاه ربات حول محوری عمود بر خود و در جا می چرخد .
- اگر سرعت از نظر مقدار متفاوت باشند ، یعنی اگر سرعت چرخ ها مقدارشان متفاوت و جهت حرکتشان نیز یکسان یا خلاف هم باشد ربات یک حرکت منحنی شکل خواهد داشت . در حالتی خاص اگر یک چرخ بچرخد و دیگری بایستد ربات حول چرخ ایستاده حرکت خواهد کرد . دستکاری مقدار سرعت و جهتِ آن می تواند مسیر های حرکت جالبی را خلق کند .
( سینماتیک عمومی )
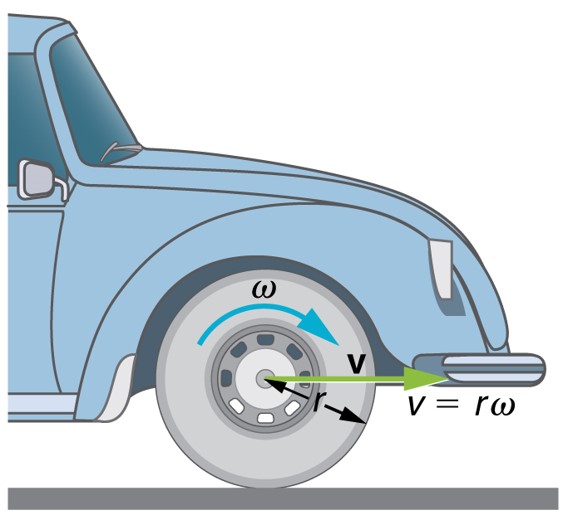
در این بخش فرمول های حرکت ربات با مکانیزم دیفرانسیلی را جهت اطلاعات تکمیلی ارائه می کنیم :
تعاریف :
سرعت زاویه ای ω : سرعت چرخش یک جسم است . بنابراین فقط برای اجسام در حال چرخش مطرح می گردد ، مثل چرخ ربات ، محور موتور ، چرخ دنده ها و اجزائی شبیه به این در ربات ها .
سرعت خطی v : سرعت حرکت اجسامی که در خطی مستقیم حرکت می کنند .
رابطه بین سرعت خطی کل ربات و سرعت زاویه ای چرخ های ربات (که البته برای هر جسم متحرکی که چرخ داشته باشد صادق است) :
v = r × ω
نکته : در برخی کتب جهت چرخش چرخ (ساعتگرد یا پاد ساعت گرد) با نگاه کردن در طرف چرخ مورد نظر به مرکز ربات اندازه گیری می شود یعنی اگر هر دو چرخ به سمت جلو حرکت کنند یکی ساعتگرد و دیگری چرخشی پاد ساعتگرد دارد.
همان طور که می دانید سرعت یک مفهوم برای اندازه گیری قابلیت طی مسافت در هر لحظه است . هر دو کمیت سرعت خطی و زاویه ای در زمان محاسبه می شوند. وقتی جسم مسیر مس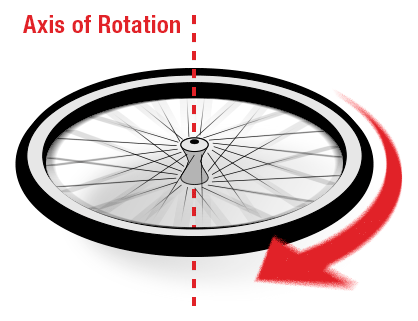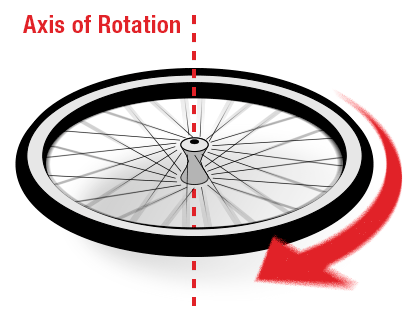 تقیم را طی می کند اندازه گیری میزان متراژ مسیر مستقیم طی شده در واحد زمان سرعت خطی و (اگر جسم متحرک شما چرخ داشته باشد) سرعت موتور ها و یا چرخ ها بر حسب تعداد دور یا زاویه ای که در واحد زمان چرخیده اند سرعت زاویه ای نام دارد. بنابراین خواهیم داشت :
تقیم را طی می کند اندازه گیری میزان متراژ مسیر مستقیم طی شده در واحد زمان سرعت خطی و (اگر جسم متحرک شما چرخ داشته باشد) سرعت موتور ها و یا چرخ ها بر حسب تعداد دور یا زاویه ای که در واحد زمان چرخیده اند سرعت زاویه ای نام دارد. بنابراین خواهیم داشت :
سرعت زاویه ای ω : تعداد دور در مدت زمان خاص ، که معمولاً در رباتیک به علت کوچک بودن مقیاس ثانیه ، واحد دقیقه را در نظر می گیرند . مثلاً در یک ربات پرنده مولتی کوپتر سرعت هر موتور حدود 5000 دور در دقیقه است ، معادل 83.3 دور در ثانیه که سرعت بسیار بالایی است و تنها با یک ملخ پلاستیکی می تواند به راحتی به دستان شما صدمه بزند! در ربات های متحرک زمینی عادی بسته به کارایی از سرعت هایی در بازه 30 تا 500 دور در دقیقه و معمولا بین 100 تا 300 دور در دقیقه استفاده می کنند .
دور در دقیقه را با RPM کوتاه شده عبارت Rotation / Revolutions Per Minute نشان می دهند .
ω = N / t
سرعت خطی v : که در فیزیک دبیرستان به خوبی با آن آشنا شده اید . جابجایی در زمانی خاص . v = dx / dt
هر چرخ در حال حرکت ، در طول یک دورِ کامل مسافتی به اندازه محیطش را روی زمین طی می کند . این مسافت دقیقاً همان خط صافی است که اگر لاستیک چرخ را خیس کنید و روی یک خط مستقیم به اندازه یک دورِ کامل روی زمین بغلتانید ردِ خیسی روی زمین باقی خواهد ماند . مثل تصویر زیر :

و یا با خیس کردن قسمتی از چرخ فاصله بین دو انتهای رد خیسیِ روی زمین ، محیط چرخ را نشان می دهد .
رابطه بین سرعت خطی کل ربات و سرعت زاویه ای چرخ های ربات (که البته برای هر جسم متحرکی که چرخ داشته باشد صادق است) :
( تعداد دور rpm × محیط چرخ m ) = سرعت خطی (متر بر دقیقه)
که تعداد دور نسبت به زمان همان سرعت زاویه ای است : ω
یعنی : V = 2πr × ω (متر بر دقیقه)
با توجه به این که سرعت های متر بر ثانیه و یا کیلو متر بر ساعت ملموس ترند بهتر است برای درک بهتر واحد سرعت را تبدیل کنید .
V(m/s)=V(m/min)/60
نکته مهم : در اغلب کتب مشاهده خواهید کرد که v = r ω و شاید کمی گیج کننده باشد که چرا بعضی ها از فرمول بالا استفاده نمی کنند . حتماً به مبحثی که سرعت زاویه ای در آن بررسی شده و واحد کمیت ها دقت کنید . در این جا واحد ما بر اساس واحد رایج در سنجش سرعت موتور و چرخ در رباتیک RPM انتخاب شده است ولی عموما در کتب مکانیک و فیزیک سرعت ω بر حسب زاویه (درجه یا رادیان) به کار می رود .
پیدا کردن سرعت و موقعیت ربات با داشتن سرعت چرخ و موقعیت اولیه :
برای اندازه گیری سرعت و موقعیت برای رباتی که در مسیر مستقیم حرکت می کند به سادگی می تونید vt = جابجایی و یا با داشتن مقدار زاویه اولیه از محور مختصات فرضی جابه جایی را به دو قسمت جابه جایی در راستای X و در راستای Y جدا کنید .
ولی برای رباتی که در حال چرخش و پیمودن مسیر منحنی است موضوع کمی متفاوت است . در این شرایط فرض می کنیم مسیر دایره ای حرکت ربات را داریم و با توجه به آن معادلات حرکت جابجایی تغییر زاویه و ... به دست می آیند .
1) رباتی را با سیستم دیفرانسیلی در فضا در نظر بگیرید . سرعت چرخ (موتور) هر سمت با زیرنویس L برای چپ (Left) و R برای راست (Right) مشخص شده است .
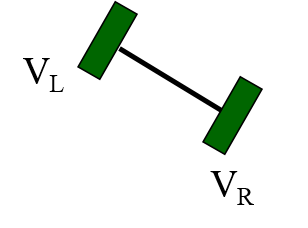
2) ابتدا یک محور مختصات در نظر بگیرید تا بر مبنای آن حرکت ربات را تحلیل کنیم . محل قرار گیری مبدا مختصات چندان مهم نیست چرا که عملا استفاده چندانی از آن نمی شود.

3) سپس یک نقطه (شعاع) فرضی که ربات دور آن در حال گردش است در نظر بگیرید . به این نقطه مرکز آنی گردش یا به اختصار ICC -instantaneous center of curvature گفته می شود .اگر لغزش چرخ ها بسیار ناچیز باشند این نقطه باید روی محور چرخش چرخ ها واقع شود .
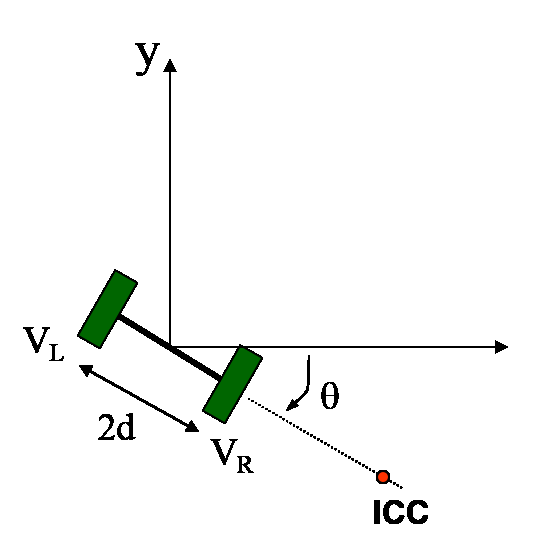
4) برای بدست آوردن سرعت چرخش ربات حول ICC با داشتن سرعت های چرخ های چپ و راست باید 2 معادله بنویسیم در هر دو معادله ω سرعت چرخش حول ICC و V ها سرعت حرکت چرخ ها هستند و از این 2 معادله و داشتن V ها می توان بدون محاسبه R به سادگی ω را به دست آورد. شعاع چرخش مرکز ربات به دور ICC را با R نشان می دهیم و شعاع چرخش هر چرخ حول ICC را با داشتن فاصله بین 2 چرخ بر مبنای R می نویسیم.
خواهیم داشت :
V(L) = (R+d) ω , V(r) = (R-d) ω
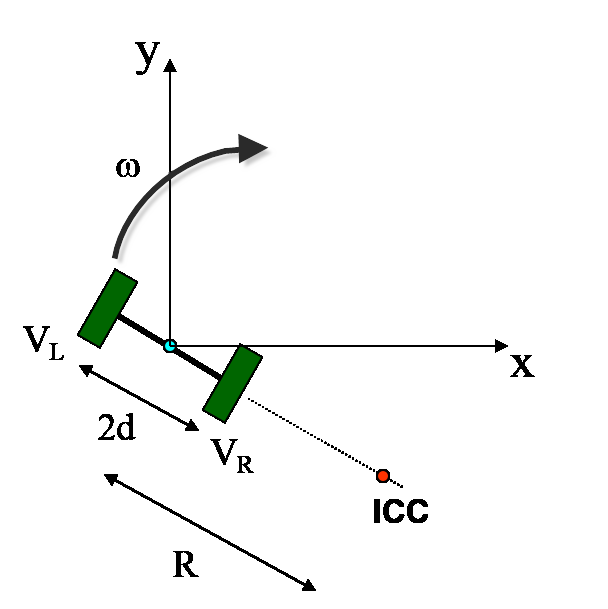
از دو رابطه بالا ω را می توان بر حسب سرعت خطی موتور یا چرخ چپ و راست نوشت . با این دو رابطه یک دستگاه دو معادله دو مجهول داریم . از آن جایی که ما همواره فاصله محوری بین دو چرخ و سرعت هر دو چرخ را داریم ولی R همیشه و به سادگی در دسترس ما نیست پس ω را بر حسب d می نویسیم و دستگاه زیر را با حذف R حل می کنیم. فقط کافی است معادله دوم را در یک منفی ضرب کرده و دو معادله را با هم جمع کنیم .
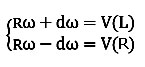
که حاصل خواهد شد : ω=(VL-VR)/2d و شعاع ربات هم با (R = 2d (VR+VL)/(VR-VL قابل محاسبه است . از مجموع روابط سرعت حرکت خود ربات برابر خواهد شد با : V = R ω = (VR+VL) / 2
با تجزیه سرعت خطی روی محور افقی x و عمودی y و اضافه کردن مثلثات می توانیم موقعیت X و Y را به صورت مجزا محاسبه کنیم .
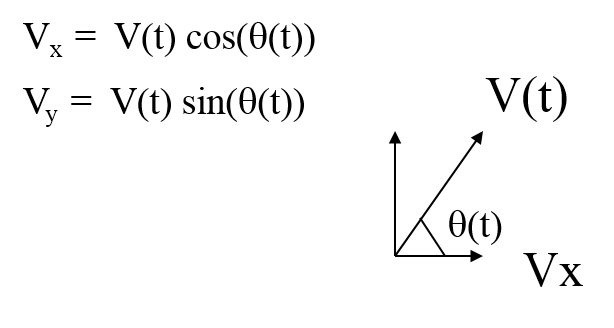
Ѳ زاویه بدنه ربات نسبت به مبدا است که مدام در حال تغییر است. در مسیر حرکت یک ربات در عمل بار ها و بار ها ω ، Ѳ و .. عوض می شوند . در نتیجه برای داشتن موقعیت نهایی باید از همه تغییرات به وجود آمده در مسیر انتگرال بگیریم ( یعنی همه تغییرات را با هم جمع کنیم ) . برای بدست آوردن زاویه ربات یا Ѳ از ضرب سرعت زاویه ای در زمان انتگرال می گیریم و برای پیدا کردن موقعیت های x و y نیز به همین شیوه عمل می کنیم .
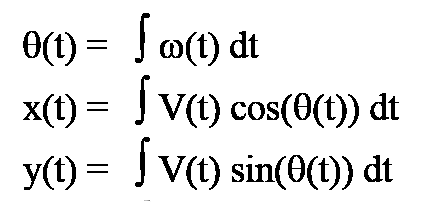
همانطور که قبلا ً V ، R و ω را به دست آوردیم . کل روابط سینماتیکی مربوط به ربات های دیفرانسیلی در این 6 رابطه خلاصه می گردد .
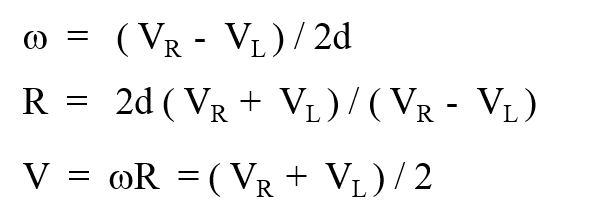
مجدداً یادآوری می کنیم که 2d فاصله بین دو چرخ (محور افقی اتصال) است که به منظور فرمول نویسی زیبا تر از ابتدا به جای d از 2d استفاده شده است .
حالا اگر یک ربات کامل با سنسور ها در دست داشته باشید که شاسی آن از نوع دیفرانسیلی است برای برنامه نویسی آن شبه برنامه ای مثل زیر را باید دنبال کنید :
خواندن ورودی سنسورها
تصمیم گیری بر اساس ورودی خوانده شده از سنسور ها
اجرای یکی از دستورالعمل های زیر :
برای حرکت مستقیم هر دو موتور (چرخ) با سرعت یکسان به جلو ؛
برای عقبگرد حرکت هر دو موتور (چرخ) با سرعت یکسان رو به عقب ؛
برای چرخش به چپ موتور سمت چپ به عقب و موتور سمت راست به جلو حرکت کند ؛
برای چرخش به راست موتور سمت راست به عقب و موتور سمت چپ به جلو حرکت کند ؛
اگر بخواهید رباتتان را حرفه ای تر کنترل کنید با دادن سرعت های مختلف به موتور چپ و راست می توانید روی یک منحنی خاص مسیر حرکت را مشخص کنید این کار معمولاً در ربات های حرفه ای و با اتصال سنسور های اندازه گیری موقعیت چرخ و کنترل PID انجام می پذیرد .
مطالب فوق برای موقعیت یابی ربات هایی مناسب است که پس از قرار گرفتن در مبدا مسیر زیادی را طی نکرده باشند . برای موقعیت یابی ربات هایی که بتوانند مسیر طولانی تری طی کنند نیاز به ملاحضات فنی بیشتری است که امیدواریم در محتواهای بعدی بتوانیم ادامه دهیم .
